Doob–Dynkin lemma

In mathematics, the Doob–Dynkin lemma, named after Joseph Doob and Eugene Dynkin, is a statement in probability theory that characterizes the situation when one random variable is a function of another, in terms of measurability and $\sigma$ algebras.

Statement of the lemma

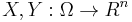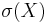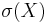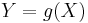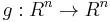Let $X,Y: \Omega \rightarrow R^n$ and $\sigma(X)$ be the $\sigma$ algebra generated by $X$ . Then $Y$ is $\sigma(X)$ measurable if and only if $Y=g(X)$ for some Borel measurable function $g:R^n\rightarrow R^n$ .

References

A. Bobrowski: Functional analysis for probability and stochastic processes: an introduction, Cambridge University Press (2005), ISBN 0-521-83166-0
M. M. Rao, R. J. Swift : Probability Theory with Applications, Mathematics and Its Applications, Band 582, Springer-Verlag (2006), ISBN 0-387-27730-7

Doob–Dynkin lemma

Statement of the lemma

References

See also